The linkage program has an interesting problem; any one simulation step starts with the mechanism in its original position and then processes the inputs to generate a new position for every link. Actuator lengths are also changed to their new lengths at the same time. What this means is that the simulator doesn’t know about any intermediate steps. Well, it knows a little bit about it because the code keep track of the last two positions of any connector and then predicts the next position. Then when the simulation code determines that a connector can be in either of two positions, the one closest to the prediction is picked.
It is important to point out why there are two possible positions for a connector.
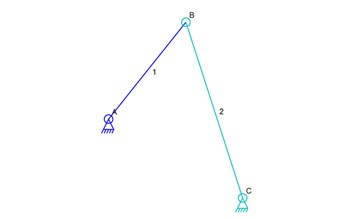
Simple Set of Connections
In the image above, there are two links labeled 1 and 2. Ignoring the position prediction feature for a moment, the simulator doesn’t really know where connector B is located. That’s because there are two places that it could be.
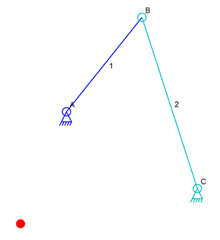
Alternate Position of B
Connector B could also be at the location of the red dot in the image above. That position is the correct distance from the anchors so that links 1 and 2 could connect there. The simulator can’t know what our human brain knows so it just picks one of those two spots, the red dot location of the connector B location that we see in the image.
Of course the simulator would not work without some sort of prediction. A simple prediction feature would be to pick the new position based on which of the two positions is closer to the previous position of B. I added the movement prediction for fun, but it usually isn’t necessary.
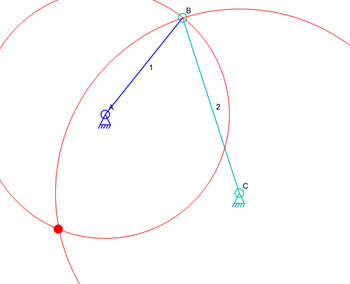
But what this shows is that simulation is not easy. It’s also not hard because the only math to connect links 1 and 2 is an equation that find the intersections of two circles, one around A and one around C.
Circle Intersections
The circle intersection is the only math used in a mechanism that has no sliding connectors. All that the simulator needs is to find two links that have one fixed connector each and one shared connector. The fixed connectors are fixed in previous simulation calculations or are anchors.
But none of this is the point of this post. The point is that the simulator can make mistakes. Consider a mechanism where each step moves a connector so far that it can move past the end of a real-world limit to a position that is valid. See, the simulator works in steps and there may be a problem where both circle intersection positions are valid but one of them is past an invalid position that was not calculated. Usually, problems of this sort happen when the mechanism moves very close to a limit.
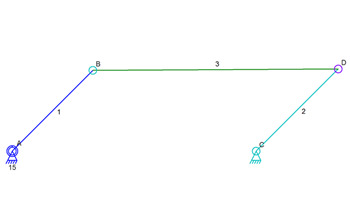
Mechanism At Start
In the image above, link 2 is just a tiny bit longer than link 1. When link 1 rotates, link 2 is pushed away. At some point, link 1 keeps rotating but begins to pull link 2 back the other way. Link 2 doesn’t keep rotating clockwise and begins to move counter-clockwise.
Mechanism Near Its Limit
The image shows the mechanism just past the limit with link 2 starting to get pulled back to the left.
If the rotation of anchor A were fast enough, it is possible that the position of connector D might end up different. It could be that link 2 keeps rotating clockwise and never reverses. The momentum prediction would likely pick that bad position, past an invalid position, as the next position in the simulation.
A user sent me a mechanism that did this every time. The solution was to slow down the movement so that the simulator didn’t accidentally pick a connector position that was wrong yet valid.
Gravity
How does this have anything to do with gravity? In a gravity simulation, the simulator takes steps. If the coder doesn’t do some complicated math and simply calculates new forces on bodies based on their current positions, gravity can get screwed up. Gravity is not linear, it is exponential. At half of the distance, gravity is not twice as strong, it is 4 times as strong. At least that’s how I remember it from when I wrote a screen saver that showed hundreds of objects all moving around on the screen and all having gravity towards each other.
Okay, so where is the problem? The problem is that the simulation might have one “planet” a bit of a distance from another and calculate the gravity, and then move the “planet” past the other so that they are incredibly close. Suddenly the gravity jump to a very large amount. In reality, the “planet” would have been that close to the other before it passed it, but the simulation has steps that in the steps, the “planet” was never that close on the one side of the other. So gravity is calculated in an unbalanced way and one “planet” passing close to another can make then fly apart or get pulled in really close to each other in unrealistic ways.
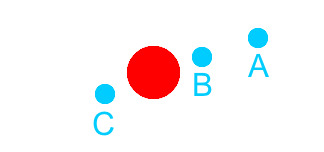
Planet Simulation Steps
In the image above, imagine that the simulator calculates gravity at position A and determines that the planet will move to position C. Since gravity is never computed at position B, the blue planet is now experiences an unbalanced gravity and is pulled towards the red sun too much.
This gravity problem is not something I ever solved because math is not my forte. But it is a problem caused by the same issue that can affect mechanical simulations. The problem is that simulators calculate discreet steps in time whereas time doesn’t. Well, some quantum physicists might argue about that but we won’t in this situation.
I wrote that gravity screen saver a long time ago. It looked cool, but sometimes the effects of the simulation steps would become apparent and objects would either fly off the screen because of one of these extreme examples of passing another body and getting very unbalanced gravity.
Intermediate Steps
My simulator animation runs at 30 frames per second. But to help with this problem, the simulator calculates 60 steps per second with two steps per frame. The intermediate step is not shown on the screen because it is only used to help make this stepping problem less obvious. If my code computed 1000 steps per animation frame, it would probably never show a problem of a link moving past an invalid location, but then the animation might slow down.
I have not tested to see how many calculations can be done in a single animation frame, but maybe it is more than a few. I’ll soon be running some tests to see if I can bump up the number a bit. Maybe it will be thousands!